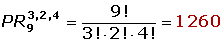Se llama permutaciones de m elementos (m = n) a las diferentes agrupaciones de esos m elementos de forma que:
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
Ejemplos
1.
Calcular las permutaciones de 6 elementos.P6 = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
2.
¿Cuántos números de 5 cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5.m = 5 n = 5
Sí entran todos los elementos. De 5 dígitos entran sólo 3.
Sí importa el orden. Son números distintos el 123, 231, 321.
No se repiten los elementos. El enunciado nos pide que las cifras sean diferentes.
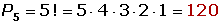
3.
¿De cuántas formas distintas pueden sentarse ocho personas en una fila de butacas?Sí entran todos los elementos. Tienen que sentarse las 8 personas.
Sí importa el orden.
No se repiten los elementos. Una persona no se puede repetir.

Permutaciones circulares
Es un caso particular de las permutaciones.
Se utilizan cuando los elementos se han de ordenar "en círculo", (por ejemplo, los comensales en una mesa), de modo que el primer elemento que "se sitúe" en la muestra determina el principio y el final de muestra.
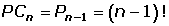
Ejemplos
1.
Calcular las permutaciones circulares de 7 elementos.PC7= (7 − 1)! = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
2.
¿De cuántas formas distintas pueden sentarse ocho personas alrededor de una mesa redonda?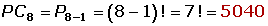
Permutaciones con repetición
Permutaciones con repetición de m elementos donde el primer elemento se repite a veces , el segundo b veces , el tercero c veces, ...(m = a + b + c + ... = n) son los distintos grupos que pueden formarse con esos m elementos de forma que :
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
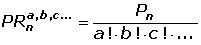
Ejemplos
Calcular las permutaciones con repetición de: 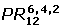
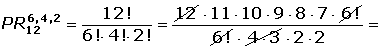
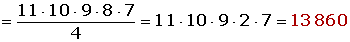
2.
Con las cifras 2, 2, 2, 3, 3, 3, 3, 4, 4; ¿cuántos números de nueve cifras se pueden formar?m = 9 a = 3 b = 4 c = 2 a + b + c = 9
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
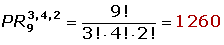
3.
En el palo de señales de un barco se pueden izar tres banderas rojas, dos azules y cuatro verdes. ¿Cuántas señales distintas pueden indicarse con la colocación de las nueve banderas?Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.