Simetría axial
Una simetría axial de eje e es una transformación, por tanto a todo punto P del plano le corresponde otro punto P' también del plano, de manera que el eje e sea la mediatriz del segmento AA'.

Las simetrías axiales son isometrías porque conservan las distancias entre los puntos y sus homólogos.

Coordenadas de un punto simétrico al eje de ordenadas
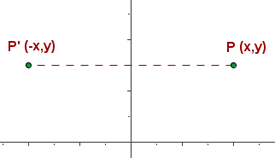
Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de ordenadas tienen sus abscisas opuestas y sus ordenadas iguales.
P(x, y) 
x = -x' y = y'
Coordenadas de un punto simétrico al eje de abscisas
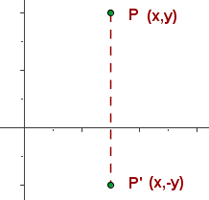
Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de abscisas tienen sus abscisas iguales y sus ordenadas opuestas.
P(x, y) 
x = x' y = -y'
Simetría de ejes paralelos
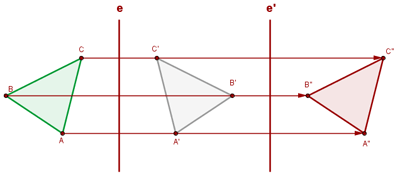
La composición de dos simetrías ejes paralelos e y e' es una traslación, cuyo vector tiene:
La longitud del vector es el doble de la distancia entre los ejes.
La dirección del vector es perpendicular a los ejes.
El sentido es el que va de e a e'.
Simetría de ejes perpendiculares
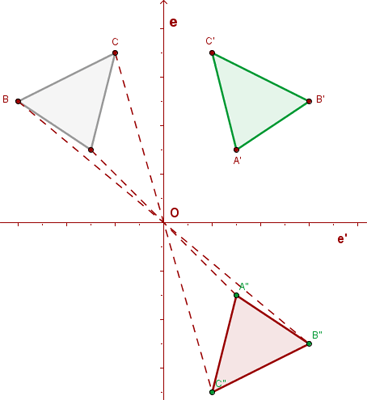
La composición de dos simetrías de ejes perpendiculares e y e' es una simetría central respecto del punto de corte de los dos ejes de simetría.
Eje de simetría
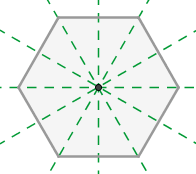
El eje de simetría de una figura es la recta que divide a la figura en dos partes iguales, de modo que define una simetría axial entre una parte y otra.
Simetría central

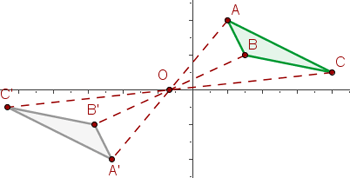
Una simetría central, de centro el punto O, es un movimiento del plano con el que a cada punto P del plano le hace corresponder otro punto P', siendo O el punto medio del segmento de extremos P y P'.
Coordenadas mediante una simetría de centro O(0,0)

Un punto P' homólogo de un punto P(x,y) mediante una simetría central de centro O(0,0) tiene de coordenadas:
Una simetría de centro O equivale a un giro de centro O y amplitud 180°.
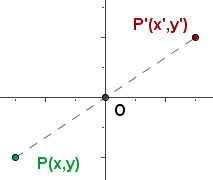
P' = (-x, -y)
x' = -x y' = -y
Coordenadas mediante una simetría de centro O(a, b)
Un punto P' homólogo de un punto P(x,y) mediante una simetría central de centro O(a ,b) tiene de coordenadas:
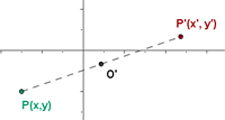
P' = (-x+ 2a, -y+ 2b)
x' = -x + 2a
y' = -y + 2b
Con el mismo centro

Como una simetría de centro O equivale a un giro de centro O y amplitud 180°, al aplicar otra transformación el ángulo será de 360°, por lo que se obtiene la misma figura, lo que se llama involución. Es una transformación involutiva.
Con distinto centro
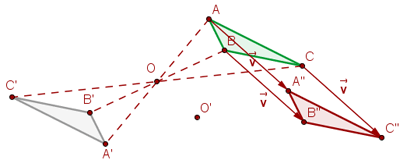
La composición de dos simetrías centrales con distinto centro es una traslación.
Centro de simetría
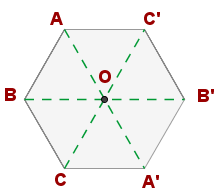
Un punto es centro de simetría de una figura si define una simetría central.

