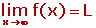Qué significa concepto de límite en Matemáticas

Límite de una sucesión

El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión

a₁= 1

a₂= 0.5

a₁₀₀₀= 0.001

a_{1000 000} = 0.000001

El límite es 0.

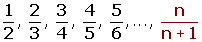
a₁= 0.5

a₂= 0.6666....

a₁₀₀₀= 0.999000999001

a_{1000 000} = 0.999999000001

El límite es 1.

a₁= 5

a₂= 7

a₁₀₀₀= 2 003

a_{1000 000} = 2 000 003

Ningún número sería el límite de esta sucesión, el límite es ∞.

Una sucesión a_n tiene por límite L si y sólo si para cualquiera número positivo ε que tomemos, existe un término a_k, a partir del cual todos los términos de a_n, siguientes a a_k cumplen que |a_n−L| < ε.

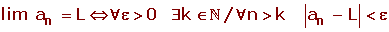
También podemos definir el límite de una sucesión mediante entornos:

Una sucesión a_n tiene por límite L si y sólo si para cualquier entorno de L que tomemos, por pequeño que sea su radio ε, existe un término de la sucesión, a partir del cual, los siguientes términos pertenecen a dicho entorno.

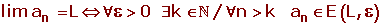
Límite de una función

El límite de la función f(x) en el punto x₀, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x₀. Es decir el valor al que tienden las imágenes cuando los originales tienden a x₀.

Vamos a estudiar el límite de la función f(x) = x² en el punto x₀ = 2.

Tanto si nos acercamos a 2 por la izquierda o la derecha las imágenes se acercan a 4.

Se dice que la función f(x) tiene como límite el número L , cuando x tiende a x₀, si fijado un número real positivo ε , mayor que cero, existe un numero positivo δ dependiente de ε , tal que, para todos los valores de x distintos de x₀ que cumplen la condición |x - x₀| < δ , se cumple que |f(x) - L| <ε .

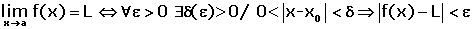
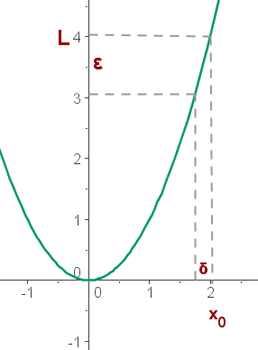
También podemos definir el concepto de límite a través de entornos:

si y sólo si, para cualquier entorno de L que tomemos, por pequeño que sea su radio , existe un entorno de x₀ , E_δ(x₀) , cuyos elementos (sin contar x₀), tienen sus imágenes dentro del entorno de L , E_ε(L).