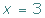Ecuaciones lineales

Ecuación lineal con n incógnitas

Una ecuación lineal con n incógnitas es cualquier expresión del tipo: a₁x₁ + a₂x₂ + a₃x₃ + ... + a_nx_n = b, donde a_i, b .

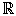
Los valores a_i se denominan coeficientes,

b es el término independiente.

Los valores x_i son las incógnitas.

Solución de una ecuación lineal

Cualquier conjunto de n números reales que verifica la ecuación se denomina solución de la ecuación.

Dada la ecuación x + y + z + t = 0, son soluciones de ella:

(1,-1,1,-1), (-2,-2,0, 4).

Ecuaciones lineales equivalentes

Son aquellas que tienen la misma solución.

x + y + z + t = 0 2x + 2y + 2z + 2t = 0

Ecuaciones lineales de primer grado

Las ecuaciones lineales de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.

Resolución de ecuaciones de primer grado

En general para resolver una ecuación de primer grado debemos seguir los siguientes pasos:

1º Quitar paréntesis.

2º Quitar denominadores.

3º Agrupar los términos en x en un miembro y los términos independientes en el otro.

4º Reducir los términos semejantes.

5º Despejar la incógnita.

Despejamos la incógnita:

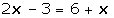
Agrupamos los términos semejantes y los independientes, y sumamos:

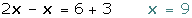
Quitamos paréntesis:

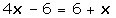
Agrupamos términos y sumamos:

Despejamos la incógnita:

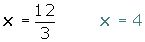
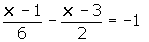
Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.

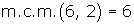
Quitamos paréntesis, agrupamos y sumamos los términos semejantes:

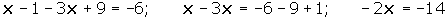
Despejamos la incógnita:

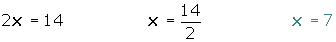
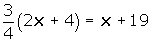
Quitamos paréntesis y simplificamos:

Quitamos denominadores, agrupamos y sumamos los términos semejantes:

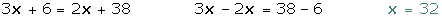
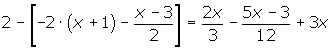
Quitamos corchete:

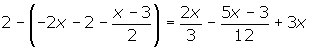
Quitamos paréntesis:

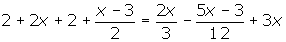
Quitamos denominadores:

Quitamos paréntesis:

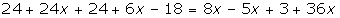
Agrupamos términos:

Sumamos:

Dividimos los dos miembros por: −9

•