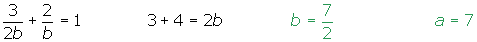La ecuación segmentaria o canónica de la recta es la expresión de la recta en función de los segmentos que ésta determina sobre los ejes de coordenadas.
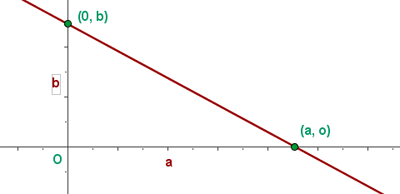

a es la abscisa en el origen de la recta.
b es la ordenada en el origen de la recta.
Los valores de a y de b se se pueden obtener de la ecuación general.
Si y = 0 resulta x = a.
Si x = 0 resulta y = b.
Una recta carece de la forma segmentaria en los siguientes casos:
1
Recta paralela a OX, que tiene de ecuación y = n.2
Recta paralela a OY, que tiene de ecuación x = k.
3
Recta que pasa por el origen, que tiene de ecuación y = mx.Ejercicios
Una recta determina sobre los ejes coordenados, segmentos de 5 y 3 unidades, respectivamente. Hallar su ecuación.
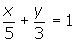
Hallar la ecuación segmentaria de la recta que pasa por P(−2, 1) y tiene por vector director v = (3, −4).
Hallamos la ecuación en forma continua:
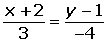
Pasamos a la general:
−4x −8 = 3y -3 4x + 3y + 5 = 0
Si y = 0 x = −5/4 = a.
Si x = 0 y = −5/3 = b.
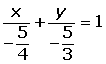
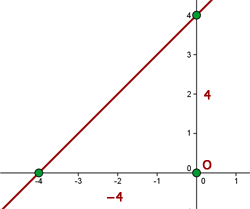
La recta r ≡ x − y + 4 = 0 forma con los ejes un triángulo del que se pide su área.
La recta forma un triángulo rectángulo con el origen y sus catetos son la abscisa y la ordenada en el origen.
Si y = 0 x = −4 = a.
Si x = 0 y = 2 = b.
La ecuación segmentaria es:
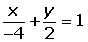
El área es:
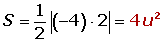
Una recta pasa por el punto A(1, 5) y determina con los ejes de coordenadas un triángulo de 18 u2 de superficie. ¿Cuál es la ecuación de la recta?
Aplicamos la ecuación segmentaria:
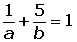
El área del triángulo es:
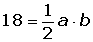
Resolvemos el sistema:





Hallar la ecuación de una recta que determina sobre los ejes coordenados, segmentos de doble longitud en el eje de abscisas, que en el de ordenadas, sabiendo que pasa por el punto A(3, 2).