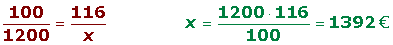Magnitud
Una magnitud es cualquier propiedad que se puede medir numéricamente.
Son magnitudes:
La longitud del lado un cuadrado.
La capacidad de una botella de agua.
Razón
Razón es el cociente entre dos números o dos cantidades comparables entre sí, expresado como fracción.

Los términos de una razón se llaman: antecedente y consecuente. El antecedente es el dividendo y el consecuente es el divisor.
Diferencia entre razón y fracción
La razón en los lados de un rectángulo de 5 cm de altura y 10 cm de base es: 
No hay que confundir razón con fracción.
Si 

Proporción
Una proporción es una igualdad entre dos razones.

Constante de proporcionalidad

Propiedades de las proporciones
En una proporción del producto de los medios es igual al producto de los extremos.

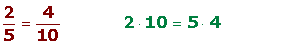
En una proporción o en una serie de razones iguales, la suma de los antecedentes dividida entre la suma de los consecuentes es igual a una cualquiera de las razones.
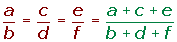
Si en una proporción cambian entre sí los medios o extremos la proporción no varía.

Cuarto proporcional
Es uno cualquiera de los términos de una proporción.
Para calcularlo se divide por el opuesto, el producto de los otros dos términos.


Medio proporcional
Una proporción es continua si tiene los dos medios iguales. Para calcular el medio proporcional de una proporción continua se extrae la raíz cuadrada del producto de los extremos.

Tercero proporcional
En una proporción continua, se denomina tercero proporcional a cada uno de los términos desiguales.
Un tercero proporcional es igual al cuadrado de los términos iguales, dividido por el término desigual.

Magnitudes directamente proporcionales
Dos magnitudes son directamente proporcionales cuando, al multiplicar o dividir una de ellas por un número cualquiera, la otra queda multiplicada o dividida por el mismo número.
Se establece una relación de proporcionalidad directa entre dos magnitudes cuando:
A más corresponde más.
A menos corresponde menos.
Son magnitudes directamente proporcionales, el peso de un producto y su precio.
Magnitudes inversamente proporcionales
Dos magnitudes son inversamente proporcionales cuando, al multiplicar o dividir una de ellas por un número cualquiera, la otra queda dividida o multiplicada por el mismo número.
Se establece una relación de proporcionalidad inversa entre dos magnitudes cuando:
A más corresponde menos.
A menos corresponde más.
Son magnitudes inversamente proporcionales, la velocidad y el tiempo:
A más velocidad corresponde menos tiempo.
A menos velocidad corresponde más tiempo.
Regla de tres directa
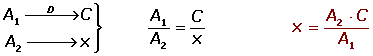
Un automóvil recorre 240 km en 3 horas. ¿Cuántos kilómetros habrá recorrido en 2 horas?
Son magnitudes directamente proporcionales, ya que a menos horas recorrerá menos kilómetros.
240 km
x km 
Regla de tres simple inversa

3 obreros construyen un muro en 12 horas, ¿cuánto tardarán en construirlo 6 obreros?
Son magnitudes inversamente proporcionales, ya que a más obreros tardarán menos horas.
3 obreros 
6 obreros 

Regla de tres compuesta
Regla de tres compuesta directa
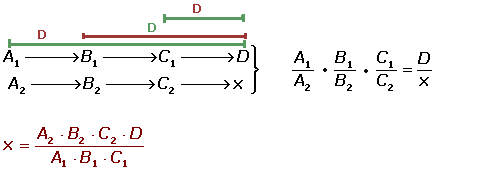
Nueve grifos abiertos durante 10 horas diarias han consumido una cantidad de agua por valor de 20 €. Averiguar el precio del vertido de 15 grifos abiertos 12 horas durante los mismos días.
9 grifos 

15 grifos 


Regla de tres compuesta inversa

5 obreros trabajando, trabajando 6 horas diarias construyen un muro en 2 días. ¿Cuánto tardarán 4 obreros trabajando 7 horas diarias?
5 obreros 
4 obreros 
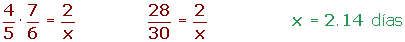
Regla de tres compuesta mixta

Si 8 obreros realizan en 9 días trabajando a razón de 6 horas por día un muro de 30 m. ¿Cuántos días necesitarán 10 obreros trabajando 8 horas diarias para realizar los 50 m de muro que faltan?
8 obreros 

10 obreros 

Repartos directamente proporcionales
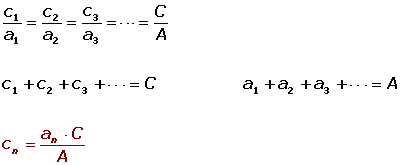
Se asocian tres individuos aportando 5000, 7500 y 9000 €. Al cabo de un año han ganado 6 450 €. ¿Qué cantidad corresponde a cada uno si hacen un reparto directamente proporcional a los capitales aportados?

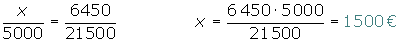
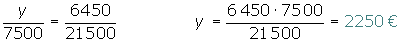
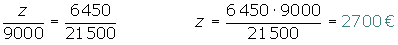
Repartos inversamente proporcionales
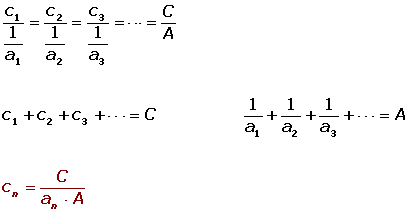
Repartir 420 €, entre tres niños en partes inversamente proporcionales a sus edades, que son 3, 5 y 6.
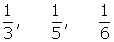
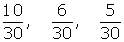
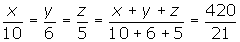
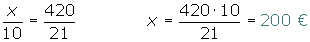
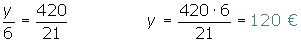

Porcentajes
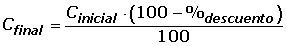
Al adquirir un vehículo cuyo precio es de 8800 €, nos hacen un descuento del 7.5%. ¿Cuánto hay que pagar por el vehículo?
100 € 
8800 € 
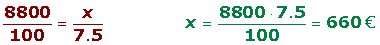
8800 € − 660 € = 8140 €
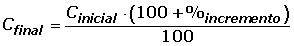
El precio de un ordenador es de 1200 € sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%?
100 € 
1200 €