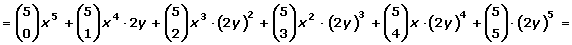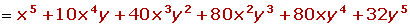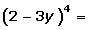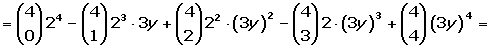Un binomio es un polinomio que consta de dos monomios.
P(x) = 2x2 + 3x
Binomio al cuadrado
Un binomio al cuadrado es igual es igual al cuadrado del primer término más, o menos, el doble producto del primero por el segundo más el cuadrado segundo.
(a + b)2 = a2 + 2 · a · b + b2
(x + 3)2 = x 2 + 2 · x ·3 + 3 2 = x 2 + 6 x + 9
(a − b)2 = a2 − 2 · a · b + b2
(2x - 3)2 = (2x)2 + 2 · 2x · 3 + 3 2 = 4x2 + 12 x + 9
Binomio al cubo
Un binomio al cubo es igual al cubo del primero más, o menos, el triple del cuadrado del primero por el segundo más el triple del primero por el cuadrado del segundo más, o menos, el cubo del segundo.
(a + b)3 = a3 + 3 · a2 · b + 3 · a · b2 + b3
(x + 3)3 = x 3 + 3 · x2 · 3 + 3 · x· 32 + 33 =
= x 3 + 9x2 + 27x + 27
(a − b)3 = a3 − 3 · a2 · b + 3 · a · b2 − b3
(2x - 3)3 = (2x)3 - 3 · (2x)2 ·3 + 3 · 2x· 32 - 33 =
= 8x 3 - 36 x2 + 54 x - 27
Diferencia de cuadrados
Una diferencia de cuadrados es igual a una suma por diferencia.
a2 − b2 = (a + b) · (a − b)
4x2 − 25 = (2x)2 − 52 = (2x + 5) · (2x - 5)
Suma de cubos
a3 + b3 = (a + b) · (a2 − ab + b2)
8x3 + 27 = (2x + 3) (4x2 - 6x + 9)
Diferencia de cubos
a3 − b3 = (a − b) · (a2 + ab + b2)
8x3 − 27 = (2x − 3) (4x2 + 6x + 9)
Producto de dos binomios que tienen un término común
(x + a) (x + b) = x2 + ( a + b) x + ab
(x + 2) (x + 3) =
= x2 + (2 + 3)x + 2 · 3 =
= x2 + 5x + 6
Binomio de Newton
La fórmula que nos permite hallar las potencias de un binomio se conoce como binomio de Newton.

Podemos observar que:
El número de términos es n+1.
Los coeficientes son números combinatorios que corresponden a la fila enésima del triángulo de Tartaglia.

En el desarrollo del binomio los exponentes de a van disminuyendo, de uno en uno, de n a cero; y los exponentes de b van aumentando, de uno en uno, de cero a n, de tal manera que la suma de los exponentes de a y de b en cada término es igual a n.
En el caso que uno de los términos del binomio sea negativo, se alternan los signos positivos y negativos.