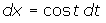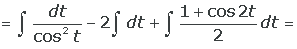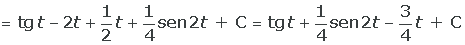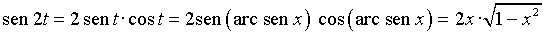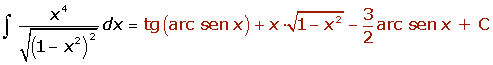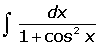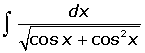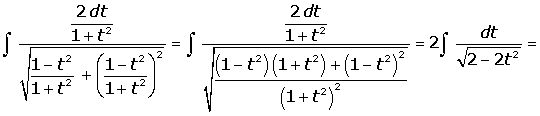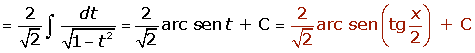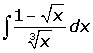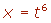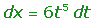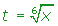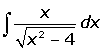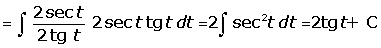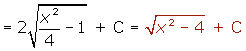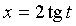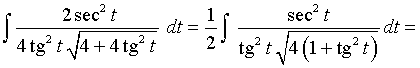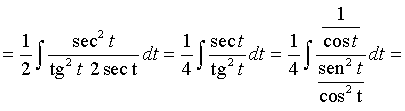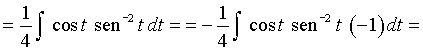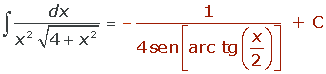Cambio de variable
El cambio de variable es una técnica que nos permite pasar de una ecuación o integral complicada a otra más sencilla.
Los cambios de variable más frecuentes se suelen dar en:
Ecuaciones y sistemas de ecuaciones exponenciales.
Cambio de variable en las ecucaciones bicuadradas
Las ecuaciones bicuadradas son ecuaciones de cuarto grado sin términos de grado impar:
ax4 + bx2 + c = 0
Para resolver ecuaciones bicuadradas, efectuamos el cambio x2 = t, x4 = t2; con lo que genera una ecuación de segundo grado con la incógnita t:
at2 + bt + c = 0
Por cada valor positivo de t habrá dos valores de x:
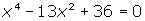
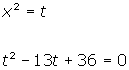
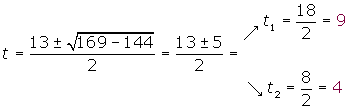
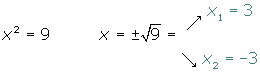
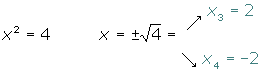
El mismo procedimiento podemos utilizar para resolver las ecuaciones del tipo:
ax6 + bx3 + c = 0
ax8 + bx4 + c = 0
ax10 + bx5 + c = 0
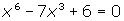
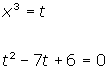
Cambio de variable en las ecucaciones y sistemas de ecuaciones exponenciales
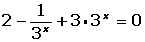
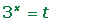
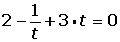
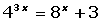
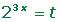
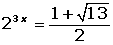
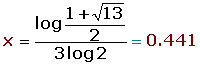
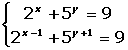
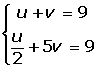
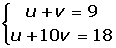
Cambio de variable en las ecucaciones logarítmicas
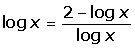
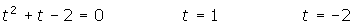
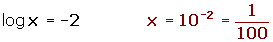
Integrales por cambio de variable
El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
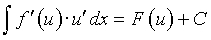
Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla.
Pasos para integrar por cambio de variable
1º Se hace el cambio de variable y se diferencia en los dos términos: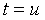
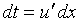
Se despeja u y dx, sutituyendo en la integral:
2º Si la integral resultante es más sencilla, integramos:
3º Se vuelve a la variable inical: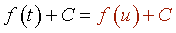
Ejemplo
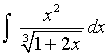
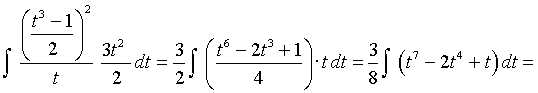
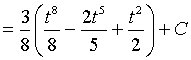
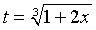
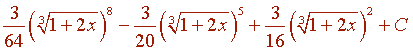
Cambios de variables
1. 
2. 
3. 
4. 
5. En las funciones racionales de radicales con distintos índices, de un mismo radicando lineal ax + b, el cambio de variable es t elevado al mínimo común múltiplo de los índices.
6. Si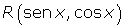 
es par:
7. Si no es par:
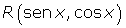
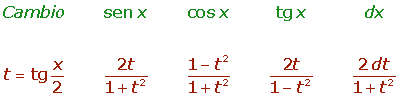
Ejemplos
