Una función es discontinua en un punto, x = a, si:
1.
El punto, x = a, no tiene imagen.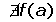
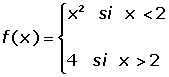
La función es discontinua en x = 2 porque no existe imagen.
2.
Que no exista el límite de la función en el punto x = a.
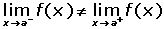
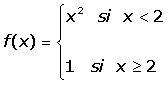
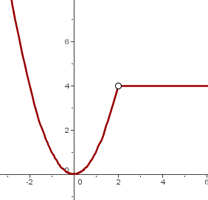
La función es discontinua en x = 2 porque no tiene límite.
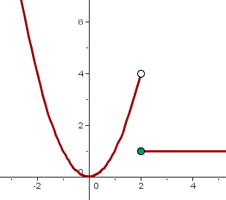
3.
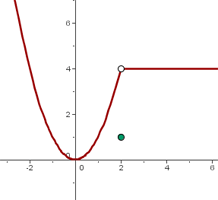
Que la imagen del punto no coincida con el límite de la función en el punto.

La función es discontinua porque en x = 2 no coincide la imagen con el límite.
Tipos de discontinuidad
Existen tres tipos de discontinuidad:
1. Discontinuidad evitable
Una discontinuidad es evitable en un punto x = a si existe 
Nos encontramos con dos tipos de discontinuidad evitable:
1.
La función no está definida en x = a.
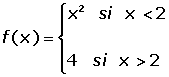

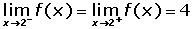

2.
La imagen no coincide con el límite.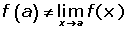

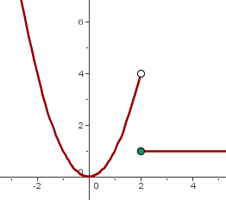
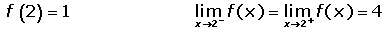
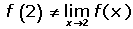
Cuando una función presenta una discontinuidad evitable en un punto se puede redefinir en dicho punto para convertirla en una función continua.
La dos funciones estudiadas anteriormente las redefinimos de modo que:
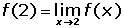

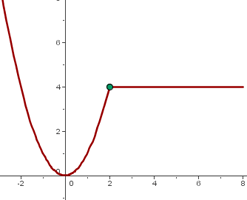
2. Discontinuidad inevitable
Una discontinuidad es inevitable o de primera especie si existen los límites laterales en x = a, pero son distintos.
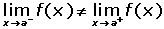
Salto
Salto es la diferencia en valor absoluto de los límites laterales.

Según el tipo de salto nos encontramos con dos tipos de discontinuidad inevitable:
1. Discontinuidad inevitable de salto finito
La diferencia entre los límites laterales es un número real.
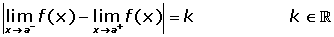


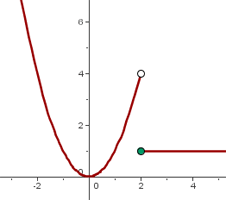
En x = 2 hay una discontinuidad inevitable de salto finito 3.
2. Discontinuidad inevitable de salto infinito
La diferencia entre los límites laterales es infinito.
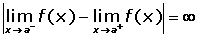



En x = 2 hay una discontinuidad inevitable de salto infinito.
3. Discontinuidad esencial
Una discontinuidad es esencial o de segunda especie si no existe alguno de los límites laterales en x = a.
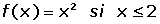

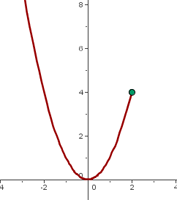
En x = 2 hay una discontinuidad esencial porque no tiene límite por la derecha.
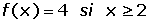

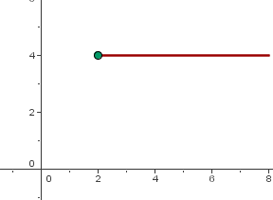
En x = 2 hay una discontinuidad esencial porque no tiene límite por la izquierda.

