La Estadística inferencial o Inferencia estadística estudia cómo sacar conclusiones generales para toda la población a partir del estudio de una muestra, y el grado de fiabilidad o significación de los resultados obtenidos.
Muestreo probabilístico
Consiste en elegir una muestra de una población al azar. Podemos distinguir varios tipos de muestreo:
Muestreo aleatorio simple
Para obtener una muestra, se numeran los elementos de la población y se seleccionan al azar los n elementos que contiene la muestra.
Muestreo aleatorio sistemático
Se elige un individuo al azar y a partir de él, a intervalos constantes, se eligen los demás hasta completar la muestra.
Por ejemplo si tenemos una población formada por 100 elementos y queremos extraer una muestra de 25 elementos, en primer lugar debemos establecer el intervalo de selección que será igual a 100/25 = 4. A continuación elegimos el elemento de arranque, tomando aleatoriamente un número entre el 1 y el 4, y a partir de él obtenemos los restantes elementos de la muestra.
2, 6, 10, 14,..., 98
Muestreo aleatorio estratificado
Se divide la población en clases o estratos y se escoge, aleatoriamente, un número de individuos de cada estrato proporcional al número de componentes de cada estrato.
En una fábrica que consta de 600 trabajadores queremos tomar una muestra de 20. Sabemos que hay 200 trabajadores en la sección A, 150 en la B, 150 en la C y 100 en la D.
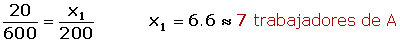
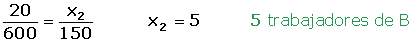


Un muestreo puede hacerse con o sin reposición, y la población de partida puede ser infinita o finita.
En todo nuestro estudio vamos a limitarnos a una población de partida infinita o a muestreo con reposición.
Si consideremos todas las posibles muestras de tamaño n en una población, para cada muestra podemos calcular un estadístico (media, desviación típica, proporción, ...) que variará de una a otra.
Así obtenemos una distribución del estadístico que se llama distribución muestral.
Si una población tiene media μ y desviación típica σ, y tomamos muestras de tamaño n (n>30, ó cualquier tamaño si la población es "normal"), las medias de estas muestras siguen aproximadamente la distribución:

Estimación de parámetros
Es el procedimiento utilizado para conocer las características de un parámetro poblacional, a partir del conocimiento de la muestra.
Con una muestra aleatoria, de tamaño n, podemos efectuar una estimación de un valor de un parámetro de la población; pero también necesitamos precisar un:
Intervalo de confianza
Se llama así a un intervalo en el que sabemos que está un parámetro, con un nivel de confianza específico.
Nivel de confianza
Probabilidad de que el parámetro a estimar se encuentre en el intervalo de confianza.
El nivel de confianza (p) se designa mediante 1 − α.
Error de estimación admisible
Que estará relacionado con el radio del intervalo de confianza.
Estimación de la media de una población
El intervalo de confianza, para la media de una población, con un nivel de confianza de 1 − α , siendo x la media de una muestra de tamaño n y σ la desviación típica de la población, es:
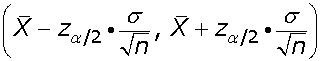
El error máximo de estimación es:

Cuanto mayor sea el tamaño de la muestra, n, menor es el error.
Cuanto mayor sea el nivel de confianza, 1-α, mayor es el error.
Tamaño de la muestra

Si aumentamos el nivel de confianza, aumenta el tamaño de la muestra.
Si disminuimos el error, tenemos que aumentar el tamaño de la muestra.
El tiempo que tardan las cajeras de un supermercado en cobrar a los clientes sigue una ley normal con media desconocida y desviación típica 0,5 minutos. Para una muestra aleatoria de 25 clientes se obtuvo un tiempo medio de 5,2 minutos.
1.
Calcula el intervalo de confianza al nivel del 95% para el tiempo medio que se tarda en cobrar a los clientes.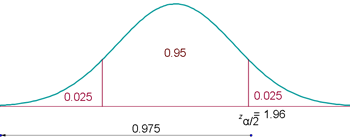
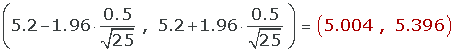
2.
Indica el tamaño muestral necesario para estimar dicho tiempo medio con un el error de ± 0,5 minutos y un nivel de confianza del 95%.
n ≥ 4
Estimación de una proporción
Si en una población, una determinada característica se presenta en una proporción p, la proporción p' , de individuos con dicha característica en las muestras de tamaño n, se distribuirán según:
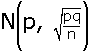
Intervalo de confianza para una proporción

El error máximo de estimación es:
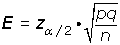
En una fábrica de componentes electrónicos, la proporción de componentes finales defectuosos era del 20%. Tras una serie de operaciones e inversiones destinadas a mejorar el rendimiento se analizó una muestra aleatoria de 500 componentes, encontrándose que 90 de ellos eran defectuosos. ¿Qué nivel de confianza debe adoptarse para aceptar que el rendimiento no ha sufrido variaciones?
p = 0.2 q = 1 - p =0.8 p'= 90/ 500 = 0.18
E = 0.2 - 0.18 = 0.02
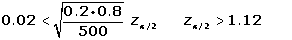
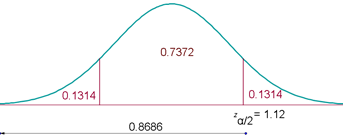
P (1 - zα/2 <1.12) = 0.86861 - 0.8686 = 0.1314
0.8686 - 0.1314 = 0.737
Nivel de confianza: 73.72%
Contraste de hipótesis
Hipótesis estadísticas
Un test estadístico es un procedimiento para, a partir de una muestra aleatoria y significativa, extraer conclusiones que permitan aceptar o rechazar una hipótesis previamente emitida sobre el valor de un parámetro desconocido de una población.
La hipótesis emitida se designa por H0 y se llama hipótesis nula.
La hipótesis contraria se designa por H1 y se llama hipótesis alternativa.
Contrastes de hipótesis
1.
Enunciar la hipótesis nula H0 y la alternativa H1.| Bilateral | H0=k | H1 ≠ k |
|---|---|---|
| Unilateral | H0≥ k | H1 < k |
| H0 ≤k | H1> k |
2.
A partir de un nivel de confianza 1 − α o el de significación α. Determinar:El valor zα/2 (bilaterales), o bien zα (unilaterales)
La zona de aceptación del parámetro muestral (x o p').
3.
Calcular: x o p', a partir de la muestra.
4.
Si el valor del parámetro muestral está dentro de la zona de la aceptación, se acepta la hipótesis con un nivel de significación α. Si no, se rechaza.
Contraste bilateral
Se presenta cuando la hipótesis nula es del tipo H0: μ = k (o bien H0: p = k) y la hipótesis alternativa, por tanto, es del tipo H1: μ≠ k (o bien H1: p≠ k).
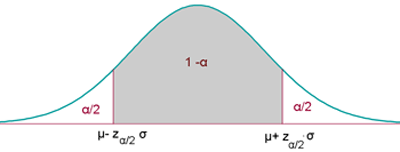
El nivel de significación α se concentra en dos partes (o colas) simétricas respecto de la media.
La región de aceptación en este caso no es más que el correspondiente intervalo de probabilidad para x o p', es decir:

o bien:
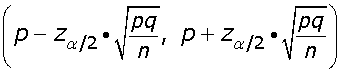
Se sabe que la desviación típica de las notas de cierto examen de Matemáticas es 2,4. Para una muestra de 36 estudiantes se obtuvo una nota media de 5,6. ¿Sirven estos datos para confirmar la hipótesis de que la nota media del examen fue de 6, con un nivel de confianza del 95%?
1.
Enunciamos las hipótesis nula y alternativa:H0 : μ = 6 La nota media no ha variado.
H1 : μ ≠ 6 La nota media ha variado.
2.
Zona de aceptaciónPara α = 0.05, le corresponde un valor crítico: zα/2 = 1.96.
Determinamos el intervalo de confianza para la media:
(6-1,96 · 0,4 ; 6+1,96 · 0,4) = (5,22 ; 6,78)
3.
Verificación.Valor obtenido de la media de la muestra: 5,6 .
4.
DecisiónAceptamos la hipótesis nula H0, con un nivel de significación del 5%.
Contraste unilateral
Caso 1
La hipótesis nula es del tipo H0: μ ≥ k (o bien H0: p ≥ k).
La hipótesis alternativa, por tanto, es del tipo H1: μ < k (o bien H1: p < k).
Valores críticos
| 1 − α | α | z α |
|---|---|---|
| 0.90 | 0.10 | 1.28 |
| 0.95 | 0.05 | 1.645 |
| 0.99 | 0.01 | 2.33 |
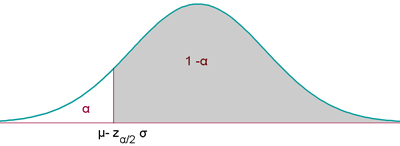
El nivel de significación α se concentra en una parte o cola.
La región de aceptación en este caso será:
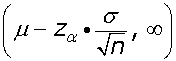
o bien:
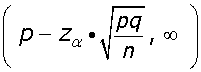
Un sociólogo ha pronosticado, que en una determinada ciudad, el nivel de abstención en las próximas elecciones será del 40% como mínimo. Se elige al azar una muestra aleatoria de 200 individuos, con derecho a voto, 75 de los cuales estarían dispuestos a votar. Determinar con un nivel de significación del 1%, si se puede admitir el pronóstico.
1.
Enunciamos las hipótesis nula y alternativa:H0 : μ ≥ 0.40 La abstención será como mínimo del 40%.
H1 : μ < 0.40 La abstención será como máximo del 40%;
2.
Zona de aceptaciónPara α = 0.01, le corresponde un valor crítico: zα = 2.33.
Determinamos el intervalo de confianza para la media:
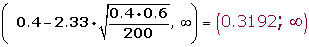
3.
Verificación.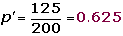
4.
DecisiónAceptamos la hipótesis nula H0. Podemos afirmar, con un nivel de significación del 1%, que la La abstención será como mínimo del 40%.
Caso 2
La hipótesis nula es del tipo H0: μ ≤ k (o bien H0: p ≤ k).
La hipótesis alternativa, por tanto, es del tipo H1: μ > k (o bien H1: p > k).
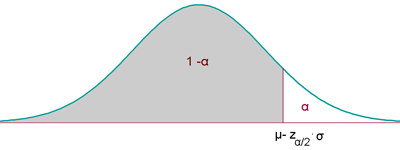
El nivel de significación α se concentra en la otra parte o cola.
La región de aceptación en este caso será:

o bien:
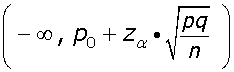
Un informe indica que el precio medio del billete de avión entre Canarias y Madrid es, como máximo, de 120 € con una desviación típica de 40 €. Se toma una muestra de 100 viajeros y se obtiene que la media de los precios de sus billetes es de 128 €.
¿Se puede aceptar, con un nivel de significación igual a 0,1, la afirmación de partida?
1.
Enunciamos las hipótesis nula y alternativa:H0 : μ ≤ 120
H1 : μ > 120
2.
Zona de aceptaciónPara α = 0.1, le corresponde un valor crítico: zα = 1.28 .
Determinamos el intervalo de confianza:

3.
Verificación.Valor obtenido de la media de la muestra: 128 € .
4.
DecisiónNo aceptamos la hipótesis nula H0. Con un nivel de significación del 10%.
Errores de tipo I y tipo II
Error de tipo I. Se comete cuando la hipótesis nula es verdadera y, como consecuencia del contraste, se rechaza.
Error de tipo II. Se comete cuando la hipótesis nula es falsa y, como consecuencia del contraste se acepta.
| H0 | Verdadera | Falsa |
|---|---|---|
| Aceptar | Decisón correcta Probabilidad = 1 − α | Decisión incorrecta: ERROR DE TIPO II |
| Rechazar | ERROR DE TIPO I Probabilidad = α | Decisión correcta |
La probabilidad de cometer Error de tipo I es el nivel de significación α.
La probabilidad de cometer Error de tipo II depende del verdadero valor del parámetro. Se hace tanto menor cuanto mayor sea n.

