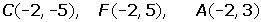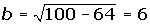Se llama ecuación reducida a la ecuación de la hipérbola cuyos ejes coinciden con los ejes coordenadas, y, por tanto, el centro de hipérbola con el origen de coordenadas.

Si el eje real está en el eje de abscisas las coordenadas de los focos son:
F'(-c,0) y F(c,0)
Cualquier punto de la hipérbola cumple:

Esta expresión da lugar a:

Realizando las operaciones y sabiendo que 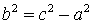
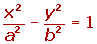
Ejemplos
Hallar la ecuación de la hipérbola de foco F(4, 0), de vértice A(2, 0) y de centro C(0, 0).
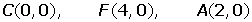


Hallar la ecuación y la excentricidad de la hipérbola que tiene como focos los puntos F'(-5, 0) y F(5, 0), y 6 como diferencia de los radios vectores.



Hallar las coordenadas de los vértices y de los focos, las ecuaciones de las asíntotas y la excentricidad de la hipérbola 9x2 - 16y2 = 144.
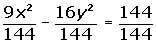
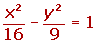




Ecuación reducida de eje vertical de la hipérbola

F'(0, -c) y F(0, c)
La ecuación será:
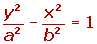
Ejemplo
Hallar la ecuación de la hipérbola de foco F(0, 5), de vértice A(0, 3) y de centro C(0, 0).
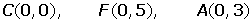


Ecuación de la hipérbola
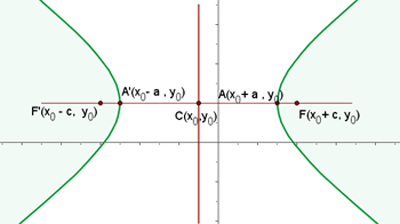
Si el centro de la hipérbola es C(x0, y0) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(X0+c, y0) y F'(X0-c, y0). Y la ecuación de la hipérbola será:
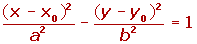
Ejemplos
Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación de la forma:

Donde A y B tienen signos opuestos.
Hallar la ecuación de la hipérbola de foco F(7, 2), de vértice A (5,2) y de centro C(3, 2).


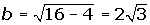
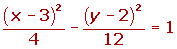
Ecuación de la hipérbola de eje vertical
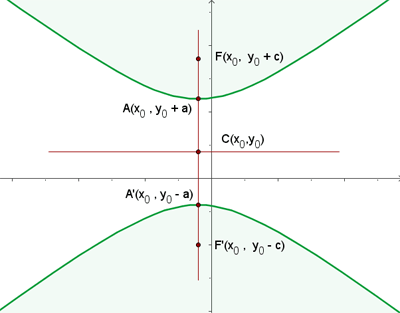
Si el centro de la hipérbola C(x0, y0) y el eje principal es paralelo a OY, los focos tienen de coordenadas F(X0, y0+c) y F'(X0, y0-c). Y la ecuación de la hipérbola será:
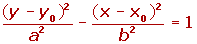
Ejemplo
Al quitar denominadores y desarrollar las ecuaciones se obtiene, en general, una ecuación de la forma:

Donde A y B tienen signos opuestos.
Hallar la ecuación de la hipérbola de foco F(-2, 5), de vértice A (-2, 3) y de centro C(-2, -5).