Construcción de parábolas a partir de y = x²
Partimos de y = x²
| x | y = x² |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |

1. Traslación vertical
y = x² + k
Si K > 0, y = x² se desplaza hacia arriba k unidades.
Si K < 0, y = x² se desplaza hacia abajo k unidades.
El vértice de la parábola es: (0, k).
El eje de simetría x = 0.
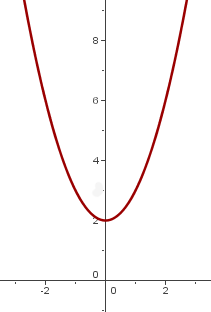
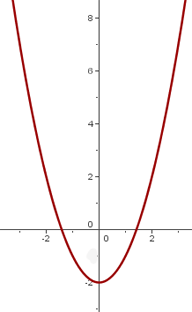
y = x² +2 y = x² -2
2. Traslación horizontal
y = (x + h)²
Si h > 0, y = x² se desplaza hacia la izquierda h unidades.
Si h < 0, y = x² se desplaza hacia la derecha h unidades.
El vértice de la parábola es: (-h, 0).
El eje de simetría es x = -h.

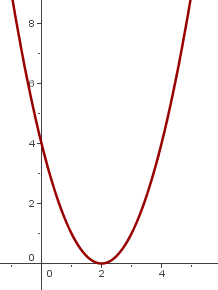
y = (x + 2)²y = (x - 2)²
3. Traslación oblicua
y = (x + h)² + k
El vértice de la parábola es: (-h, k).
El eje de simetría es x = -h.
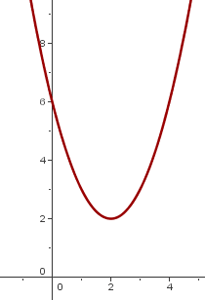
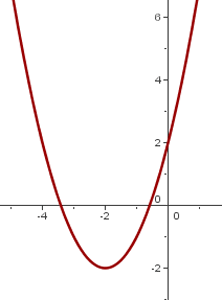
y = (x - 2)² + 2 y = (x + 2)² − 2

