Dados dos conjuntos A y B, llamamos función a la correspondencia de A en B en la cual todos los elementos de A tienen a lo sumo una imagen en B, es decir una imagen o ninguna.
Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real.
f : D 
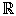
x 
El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.
El número x perteneciente al dominio de la función recibe el nombre de variable independiente.
Al número, y, asociado por f al valor x, se le llama variable dependiente. La imagen de x se designa por f(x). Luego
y= f(x)
Se denomina recorrido de una función al conjunto de los valores reales que toma la variable y o f(x).
x 
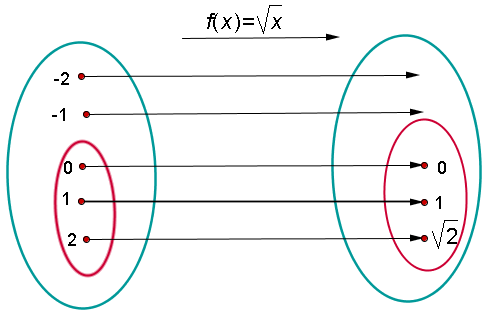
Conjunto inicial Conjunto final
Dominio Conjunto imagen o recorrido
El dominio es el conjunto de elementos que tienen imagen.
D = {x 
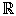

El recorrido es el conjunto de elementos que son imágenes.
R = {f (x) / x 
D = {x 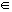
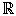
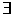
Dominio de la función polinómica entera
El dominio es R, cualquier número real tiene imagen.
f(x)= x2 - 5x + 6 D=R
Dominio de la función racional
El dominio es R menos los valores que anulan al denominador (no puede existir un número cuyo denominador sea cero).


Dominio de la función irracional de índice impar
El dominio es R.


Dominio de la función irrracional de índice par
El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
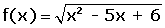


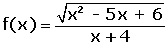

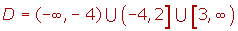
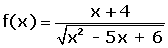

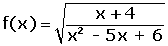

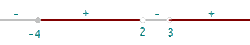
Dominio de la función logarítmica
El dominio está formado por todos los valores que hacen que el radicando sea mayor que cero.
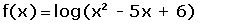

Dominio de la función exponencial
El dominio es R.
Dominio de la función seno
El dominio es R.
Dominio de la función coseno
El dominio es R.
Dominio de la función tangente
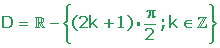

Dominio de la función cotangente


Dominio de la función secante

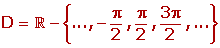
Dominio de la función cosecante


Dominio de operaciones con funciones
Si relizamos operaciones con funciones, el dominio de la función resultante será:

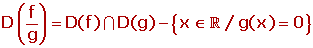
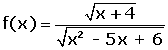



Gráfica de funciones
Si f es una función real, a cada par (x, y) = (x, f(x)) determinado por la función f le corresponde en el plano cartesiano un único punto P(x, y) = P(x, f(x)). El valor de x debe pertenecer al dominio de definición de la función.
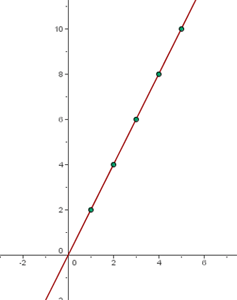
Como el conjunto de puntos pertenecientes a la función es ilimitado, se disponen en una tabla de valores algunos de los pares correspondientes a puntos de la función. Estos valores, llevados sobre el plano cartesiano, determinan puntos de la gráfica. Uniendo estos puntos con línea continua se obtiene la representación gráfica de la función.
| Kg de patatas | Precio en € |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
Grafo de una función
Grafo de una función es el conjunto de pares formados por los valores de la variable y sus imágenes correspondientes.
G(f) = {x, f(x) /x