Múltiplos
Un número es múltiplo de otro si lo contiene varias veces exactamente.
Un número a es múltiplo de otro b cuando es el resultado de multiplicarlo por otro número c.
Un número b es un divisible por otro a cuando la división es exacta.
14 es múltiplo de dos, ya que resulta de multiplicar 2 por 7.
14 = 2 · 7
Divisores
Un número es divisor de otro cuando lo divide exactamente.
3 es divisor de 15; 15 : 3 = 5.
A los divisores también se les llama factores.
Divisibilidad
Un número b es un divisible por otro a cuando la división es exacta.
Criterios de divisibilidad
2
Un número es divisible por 2, si termina en cero o cifra par.
24, 238, 1024.
3
Un número es divisible por 3, si la suma de sus dígitos nos da múltiplo de 3.
564
5 + 6 + 4 = 15, es mútiplo de 3
2040
2 + 0 + 4 + 0 = 6, es mútiplo de 3
5
Un número es divisible por 5, si termina en cero o cinco.
45, 515, 7525.
7
Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó múltiplo de 7.
343
34 - 2 · 3 = 28, es mútiplo de 7
105
10 - 5 · 2 = 0
2261
226 - 1 · 2 = 224
Volvemos a repetir el proceso con 224.
22 - 4 · 2 = 14, es mútiplo de 7.
11
Un número es divisible por 11, si la diferencia entre la suma de las cifras que ocupan los lugares pares y la de los impares es 0 ó múltiplo de 11.
121
(1 + 1) - 2 = 0
4224
(4 + 2) - (2 + 4) = 0
Otros criterios de divisblilidad
4
Un número es divisible por 4, si sus dos últimas cifras son ceros o múltiplo de 4.
36, 404, 1 028.
6
Un número es divisible por 6, si es divisible por 2 y por 3.
72, 324, 2 400
8
Un número es divisible por 8, si sus tres últimas cifras son ceros o múltiplo de 8.
4000, 1048, 1 512.
9
Un número es divisible por 9, si la suma de sus dígitos nos da múltiplo de 9.
81
8 + 1 = 9
3663
3 + 6 + 6 + 3 = 18, es mútiplo de 9
10
Un número es divisible por 10, si la cifra de las unidades es 0.
130, 1440, 10 230
25
Un número es divisible por 25, si sus dos últimas cifras son ceros o múltiplo de 25.
500, 1025, 1875.
125
Un número es divisible por 125, si sus tres últimas cifras son ceros o múltiplo de 125.
1000, 1 125, 4 250.
Factorización
Para factorizar un número o descomponerlo en factores efectuamos sucesivas divisiones entre sus divisores primos hasta obtener un uno como cociente.
Para realizar las divisiones utilizaremos una barra vertical, a la derecha escribimos los divisores primos y a la izquierda los cocientes.
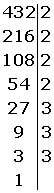
432 = 24 · 33
Números primos
Un número primo sólo tiene dos divisores: él mismo y la unidad.
5, 13, 59.
El número 1 sólo tiene un divisor, por eso no lo consideramos primo.
Para averiguar si un número es primo, se divide ordenadamente por todos los números primos menores que él. Cuando, sin resultar divisiones exactas, llega a obtenerse un cociente menor o igual al divisor, se dice que el número es primo.

Por tanto 179 es primo.
Número compuesto
Un número compuesto posee más de dos divisores.
12, 72, 144.
Los números compuestos, se pueden expresar como productos de potencias de números primos, a dicha expresión se le llama descomposición de un número en factores primos.
70 = 2 ·5 · 7
El máximo común divisor (m.c.d. o mcd) de dos o más números es el mayor número que divide a todos exactamente.
Cálculo del máximo común divisor
1.
Se descomponen los números en factores primos.2.
Se toman los factores comunes con menor exponente.Hallar el m. c. d. de: 72, 108 y 60.
1.

72 = 23 · 32
108 = 22 · 33
60 = 22 · 3 · 5
2.
m. c. d. (72, 108, 60) = 22 · 3 = 12
12 es el mayor número que divide a 72, 108 y 60.
Si un número es divisor de otro, entonces éste es el m. c. d.
El número 12 es divisor de 36.
m. c. d. (12, 36) = 12
El algoritmo de Euclides es un procedimiento para calcular el m.c.d. de dos números. Los pasos son:
1.
Se divide el número mayor entre el menor.2.
Si:
1.
La división es exacta, el divisor es el m.c.d.2.
La división no es exacta, dividimos el divisor entre el resto obtenido y se continúa de esta forma hasta obtener una división exacta, siendo el último divisor el m.c.d.m. c. d. (72, 16)
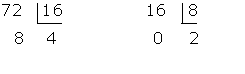
m. c. d. (72, 16) = 8
El mínimo común múltiplo es el menor de todos múltiplos comunes a varios números, excluido el cero.
Cálculo del mínimo común múltiplo
1.
Se descomponen los números en factores primos2.
Se toman los factores comunes y no comunes con mayor exponente.Hallar el m. c. m. de: 72, 108 y 60.
72 = 23 · 32
108 = 22 · 33
60 = 22 · 3 · 5
m. c. m. (72, 108, 60) = 23 · 33 · 5 = 1 080
1 080 es el menor número que divide a: 72, 108 y 60.
Si un número es un múltiplo de otro, entonces es el m. c. m. de ambos.
El número 36 es múltiplo de 12.
m. c. m. (12, 36) = 36
Relación entre el m. c. d. y m. c. m.
m. c. d. (a, b) · m. c. m. (a, b) = a · b

