La esperanza matemática o valor esperado de una variable aleatoria discreta es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso.
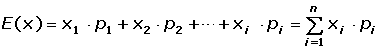
Los nombre de esperanza matemática y valor esperado tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.
Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.
Ejemplos
Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?
E(x) = 5000 · 0.001 + 2000 · 0.003 = 11 €
Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.
E = {(c,c);(c,x);(x,c);(x,x)}
p(+1) = 2/4
p(+2) = 1/4
p(−5) = 1/4
E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = −1/4. Es desfavorable

