Qué significa recta tangente en Matemáticas

Pendiente

La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto.

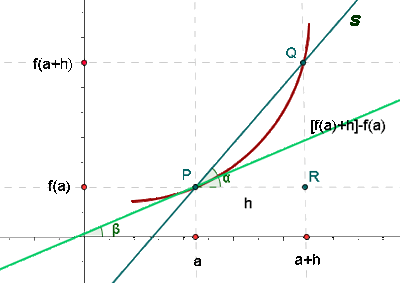
Ecuación de la recta tangente

La recta tangente a a una curva en un punto es aquella que pasa por el punto (a, f(a)) y cuya pendiente es igual a f '(a).

Problemas

Calcular los puntos en que la tangente a la curva y = x³ − 3x² − 9x + 5 es paralela al eje OX.

y^' = 3x² − 6x − 9;     x² − 2x − 3 = 0 (simplificando por 3)

x₁ = 3 y₁ = −22

x₂ = −1y₂ = 10

A(3, −22) B(−1, 10)

Se ha trazado una recta tangente a la curva y= x³, cuya pendiente es 3 y pasa por el punto (0,−2). Hallar el punto de tangencia.

Sea el punto de tangencia (a, f(a))

f' (x)= 3x²f' (a)= 3a²

3a²=3a = ±1

Las ecuaciones de la rectas tangentes son:

a = 1 f(a) = 1

y − 1 = 3(x − 1) y = 3x−2

a = −1 f(a) = −1

y + 1= 3(x + 1) y = 3x + 2   

El punto (0, −2) pertenece a la recta  y = 3x−2.

Por tanto el punto de tangencia será (1, 1) .

Encontrar los puntos de la curva f(x) = x⁴ + 7x³ + 13x² + x +1, para los cuales la tangente forma un ángulo de 45º con OX.

m = 1

f'(x) = 4x³ + 21x² + 26x +1

4x³ + 21x² + 26x +1 = 1

x = 0 x = −2 x z= 13/4

P(0, 4) Q(−2, 4) R(13/4, 1621/256)

Dada la función f(x) = tg x, hallar el ángulo que forma la recta tangente a la gráfica de la función f(x) en el origen, con el eje de abscisas.

f′(x) = 1 + tg² x       f′(0) = 1 = m

y = x

α = arc tg 1 = 45º

Hallar los coeficientes de la ecuación y = ax² + bx + c, sabiendo que su gráfica pasa por (0, 3) y por (2, 1)., y en este último punto su tangente tiene de pendiente 3.

Pasa por (0, 3) 3 = c

Pasa por (2, 1) 1= 4a + 2b + c

y^' = 2ax + b 3 = 4a + b

Resolviendo el sistema se obtiene:

a = 2 b = −5 c = 3

La gráfica de la función y = ax² + bx + c pasa por los puntos (2, 3) y (3, 13). siendo la tangente a la misma en el punto de abscisa 1 paralela a la bisectriz del primer cuadrante. Hallar el valor numérico de a, b y c.

Pasa por (2, 3) 3 = 4a + 2b + c

Pasa por (3, 13)13 = 9a + 3b +c

y^' = 2ax + b 1 = 2a + b

Resolviendo el sistema se obtiene:

a = 3 b = −5 c =1

Dada la función  f(x) = ax³ + bx² + cx + d, determina a, b, c y d; sabiendo que la curva pasa por los puntos (−1, 2) (2, 3), y que las tangentes a ellas en los puntos de abscisa 1 y −2 son paralelas al ejes de abscisas.

f(−1) = 2 −a + b − c + d = 2

f(2) = 3 8a + 4b + 2c + d = 3

f′(−1) = 0 3a + 2b + c = 0

f′(2) = 0 12a − 4b + c = 0

a = − 2 /9 b = − 1 /3 c = 4/3 d = 31/9