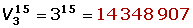Variaciones ordinarias
Se llama variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos de forma que:
No entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.
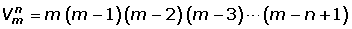
También podemos calcular las variaciones mediante factoriales:
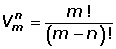
Las variaciones se denotan por 
Ejemplos
1.
Calcular las variaciones de 6 elementos tomados de tres en tres.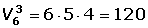
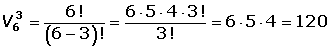
2.
¿Cuántos números de tres cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5 ?m = 5n = 3 m ≥ n
No entran todos los elementos. De 5 dígitos entran sólo 3.
Sí importa el orden. Son números distintos el 123, 231, 321.
No se repiten los elementos. El enunciado nos pide que las cifras sean diferentes.
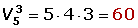
3.
¿Cuántos números de tres cifras diferentes se puede formar con los dígitos: 0, 1, 2, 3, 4, 5 ?m = 6n = 3 m ≥ n
Tenemos que separar el número en dos bloques:

El primer bloque, de un número, lo puede ocupar sólo uno de 5 dígitos porque un número no comienza por cero (excepto los de las matriculas, los de la lotería y otros casos particulares),
m = 5 n = 1
El segundo bloque, de dos números, lo puede ocupar cualquier dígito.
m = 6 n = 2
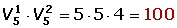
4.
A un concurso literario se han presentado 10 candidatos con sus novelas. El cuadro de honor lo forman el ganador, el finalista y un accésit.¿Cuántos cuadros de honor se pueden formar?m = 10n = 3
No entran todos los elementos. De 10 candidatos entran sólo 3.
Sí importa el orden. No es lo mismo quedar ganador que finalista.
No se repiten los elementos. Suponemos que cada candidato presenta una sola obra.
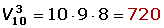
Variaciones con repetición
Se llamann variaciones con repetición de m elementos tomados de n en n a los distintos grupos formados por n elementos de manera que:
No entran todos los elementos si m > n. Sí pueden entrar todos los elementos si m ≤ n
Sí importa el orden.
Sí se repiten los elementos.
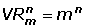
Ejemplos
1.
¿Cuántos números de tres cifras se puede formar con los dígitos: 1, 2, 3, 4, 5 ?m = 5 n = 3
No entran todos los elementos. De 5 dígitos entran sólo 3.
Sí importa el orden. Son números distintos el 123, 231, 321.
Sí se repiten los elementos. El enunciado nos pide que las cifras sean diferentes.

2.
¿Cuántos números de tres cifras se puede formar con los dígitos: 0, 1, 2, 3, 4, 5 ?m = 6 n = 3
Tenemos que separar el número en dos bloques:

El primer bloque, de un número, lo puede ocupar sólo uno de 5 dígitos porque un número no comienza por cero (excepto los de las matriculas, los de la lotería y otros casos particulares),
m = 5 n = 1
El segundo bloque, de dos números, lo puede ocupar cualquier dígito.
m = 6 n = 2

3.
¿Cuántas quinielas de una columna han de rellenarse para asegurarse el acierto de los 15 resultados?m = 3 n = 15 m < n
Sí entran todos los elementos. En este caso el número de orden es mayor que el número de elementos.
Sí importa el orden.
Sí se repiten los elementos.