La Combinatoria estudia las ordenaciones o agrupaciones de un determinado número de elementos.
En todo problema combinatorio hay varios conceptos claves que debemos distinguir:
1. Población
Es el conjunto de elementos que estamos estudiando. Denominaremos con m al número de elementos de este conjunto.
2. Muestra
Es un subconjunto de la población. Denominaremos con n al número de elementos que componen la muestra.
Los diferentes tipos de muestra vienen determinados por dos aspectos:
Orden
Es decir, si es importante que los elementos de la muestra aparezcan ordenados o no.
Repetición
La posibilidad de repetición o no de los elementos.
Factorial de un número natural
Es el producto de los “n” factores consecutivos desde “n” hasta 1. El factorial de un número se denota por n!.
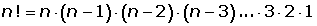
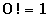

Variaciones
Variaciones ordinarias
Se llama variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos de forma que:
No entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.


También podemos calcular las variaciones mediante factoriales:

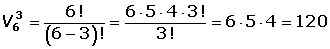
Las variaciones se denotan por 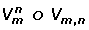
Variaciones con repetición
Se llamann variaciones con repetición de m elementos tomados de n en n a los distintos grupos formados por n elementos de manera que:
No entran todos los elementos si m > n. Sí pueden entrar todos los elementos si m ≤ n
Sí importa el orden.
Sí se repiten los elementos.


Permutaciones
Se llama permutaciones de m elementos (m = n) a las diferentes agrupaciones de esos m elementos de forma que:
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.

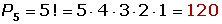
Permutaciones circulares
Es un caso particular de las permutaciones.
Se utilizan cuando los elementos se han de ordenar "en círculo", (por ejemplo, los comensales en una mesa), de modo que el primer elemento que "se sitúe" en la muestra determina el principio y el final de muestra.
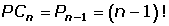
PC7= (7 − 1)! = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Permutaciones con repetición
Permutaciones con repetición de m elementos donde el primer elemento se repite a veces , el segundo b veces , el tercero c veces, ...(m = a + b + c + ... = n) son los distintos grupos que pueden formarse con esos m elementos de forma que :
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
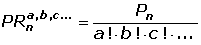

Combinaciones
Se llama combinaciones de m elementos tomados de n en n (m ≥ n) a todas las agrupaciones posibles que pueden hacerse con los m elementos de forma que:
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.
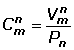
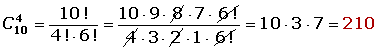
También podemos calcular las combinaciones mediante factoriales:
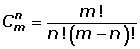
Las combinaciones se denotan por 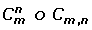
Combinaciones con repetición
Las combinaciones con repetición de m elementos tomados de n en n (m ≥ n), son los distintos grupos formados por n elementos de manera que:
No entran todos los elementos.
No importa el orden.
Sí se repiten los elementos.
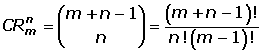
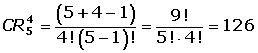
Números combinatorios
El número 

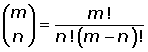

Propiedades de los números combinatorios
1.
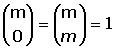
2.
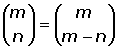
Los números de este tipo se llaman complementarios.
3.

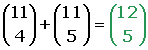
El triángulo de números combinatorios de Tartaglia o de Pascal (debido a que fue este matemático quien lo popularizó) es un triángulo de números enteros, infinito y simétrico, del que podemos ver sus primeras líneas:

Propiedades del Triángulo de Pascal o de Tartaglia
1.
La primera fila corresponde a los números combinatorios de 1, el número superior es un 1, la segunda de 2, la tercera de 3 y así sucesivamente.2.
Todas la filas empiezan y acaban en 1.

3.
Todas las filas son simétricas.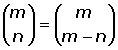
4.
Cada número se obtiene sumando los dos que están situados sobre él.Aplicando estas propiedades podemos escribir el triángulo de Pascal:
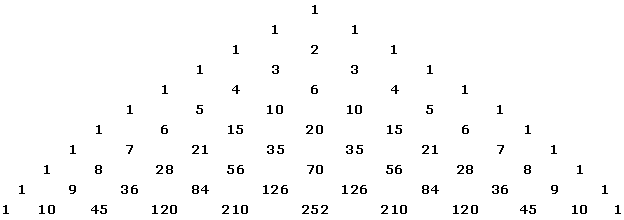
El triángulo de Pascal o de Tartaglia nos será muy útil para calcular los coefecientes del binomio de Newton.

